现在的位置:主页 > 期刊导读 >
进化粒子群算法在航空发动机模型求解中的应用
【作者】:admin【关键词】:【摘要】:航空发动机模型在航空发动机设计、性能分析、健康管理以及控制研制中都发挥着重要作用。好的模型能大幅度缩短研制周期,节约成本。求解发动机数学模型,在数学上可等价为求解
航空发动机模型在航空发动机设计、性能分析、健康管理以及控制研制中都发挥着重要作用。好的模型能大幅度缩短研制周期,节约成本。求解发动机数学模型,在数学上可等价为求解非线性最小二乘问题。传统优化算法往往需要目标函数连续可导,而发动机部件级模型本身非常复杂,传统的优化算法对迭代的初值依赖过高、易陷入局部最小等问题非常突出,制约了精确的发动机模型与仿真的发展[1]。近年来,以粒子群为代表的各种基于随机搜索的现代化算法得到迅速发展,该算法无需目标函数梯度信息,具有结构简单、易于实现和参数少等优点,在求解一些复杂的多维问题上比传统优化算法具有更大的优势[2-3]。
粒子群算法从随机解出发,通过迭代寻找最优解,并通过适应度函数评价解的品质。在每次迭代中,粒子通过跟踪两个极值来更新自己的位置。第一个极值是整个种群目前找到的最优解,另一个极值是整个种群目前找到的最优解,为全局极值。粒子在运动的过程中每个个体都会参照全局最优位置的粒子,粒子的独立性较差,所有的粒子都去追随优秀个体,很容易使算法陷入局部最优,而当前的标准粒子群算法并没有避免这一问题。在粒子搜索过程中,如果其解空间较小,维度低情况下,可存在的局部最优较小,标准粒子群算法能很有效率地解决问题,但当遇到复杂的高维问题,会使计算复杂度爆炸式增长,导致计算无法求解。为了改进粒子群算法的随机性和搜索能力,有国外学者提出,将进化算法的“变异、重组”等思想引进粒子群算法,为进化粒子群算法(EPSO)。许多实例已经证明,进化粒子群算法优于其他经典方法[4-5]。本文将进化粒子群算法应用于典型的涡扇发动机部件级非线性模型求解中,显著地提高了计算的精度和收敛性。
1??基于进化粒子群算法的发动机非线性模型求解
1.1??进化粒子群算法
进化粒子群算法(EPSO)是一种混合方法,将进化算法的“变异、重组”等思想引进粒子群算法。
进化粒子群算法的基本操作是:
番茄灰霉病发生特点及室内毒力测定 …………………… 张庆萍,王燕春,王秀琴,田晓燕,赵伟强,徐 佳,邱廷艳,龚 静(69)
(1)复制:将种群内的每个粒子复制r次;
2.2 近期疗效 术后6周,观察组患者临床总有效率为79.2%,对照组为62.5%,两组比较,差异无统计学意义(P>0.05)。见表2。
(2)变异:种群中每个粒子都有它的变异策略参数;
(3)生殖:每一个变异粒子通过粒子群算法的移动规则重组产生一个后代;
在EPSO算法中,复制时期生成的r个克隆粒子,它们的策略参数处于变异中,然后再进行重新组合操作(移动规则同PSO算法),在r个不同位置生成r个后代,对这些后代进行选择操作并且选择一个最优的后代存活下来作为下一代种群中的粒子。对原种群中每个个体重复这一过程。算法流程如图1所示。
(5)选择:通过随机对比或者其他选择程序,留下最佳的粒子,所有的粒子的最优后代集合在一起,成为下一代种群。
wi4是每个粒子的第四个策略参数,该参数控制当前全局最优的分布,假设真正的全局最优还没有找到时可以使得它的邻域可以被搜索到。
可蔓突然放声大笑起来。可蔓一笑,那几个八路军也笑了。八路军一笑,地上日本兵一个个都爬起来了,跟着一起笑。一伙人正笑着,周青也被一个日本兵攀着肩膀走进来了。一伙人又是一阵大笑。
给出一个在k代的粒子,k+1代粒子由式(1)给出:
其中:pi是粒子i从开始到当前这一代的最佳点,pg是整个种群的粒子从开始到当前代的最佳点,xi(k)是处于k代的粒子i,vi(k)是粒子i在k代的速度,wi1是粒子的惯性权重因子,wi2是粒子记忆权重因子,wi3是粒子信息交换权重因子,P是交流因子,p值是一个外部参数,控制种群信息的通路,通常其值为1。公式中符号*代表那些参数处于演化阶段。
一般来说,春秋无义战,但有两次,其中就包括鲁庄公战齐师于乾时之战。作战失败,《春秋》违反了“内不言败”的通例而直书“败绩”,原因在于褒奖鲁庄公为复仇而战,故大力彰显。因此,公羊学认为,勇于复仇,这是大义所在,已值得肯定,即使战败,也是光荣的。
不注重阅读与写作的结合是语文教学中常出现的问题。其实,教材是很好的例子,老师要引导学生从中汲取写作的养分,学习名家的谋篇布局、学习作者表现手法的运用、学习品味经典优美的语言,从而提高写作水平。例如在学完鲁迅先生写的《藤野先生》一文,可以指导学生学习用具体典型的事件来反映人物性格特点与人物品格的写作方法;学完《海燕》一文,可以指导学生将正面描写与侧面描写相结合来刻画所描写的人与物,以更好地突出所要描写的人与物鲜明的个性特点。
当共同工作方程6个残差值趋于0时,认为模型获得可靠解。在应用进化粒子群算法求解时,同经典方法一样,需要设计点参数和初值。计算流程如图2所示。
权重的变化由学习参数τ调节。
本文以通用双转子涡扇发动机为例,取低压百分比转速(PCNF)、风扇工作点位置参数(ZF)、高压百分比转速(PCNC)、压气机工作点位置参数(ZC)、高压涡轮流量函数(TFFHP)、低压涡轮流量函数(TFFLP)为独立变量,通过部件级热力学方程联立求解共同工作方程组:
生殖过程中所采用的粒子重组和移动规则如下:
(4)评估:每一个后代都有它的适应度函数;
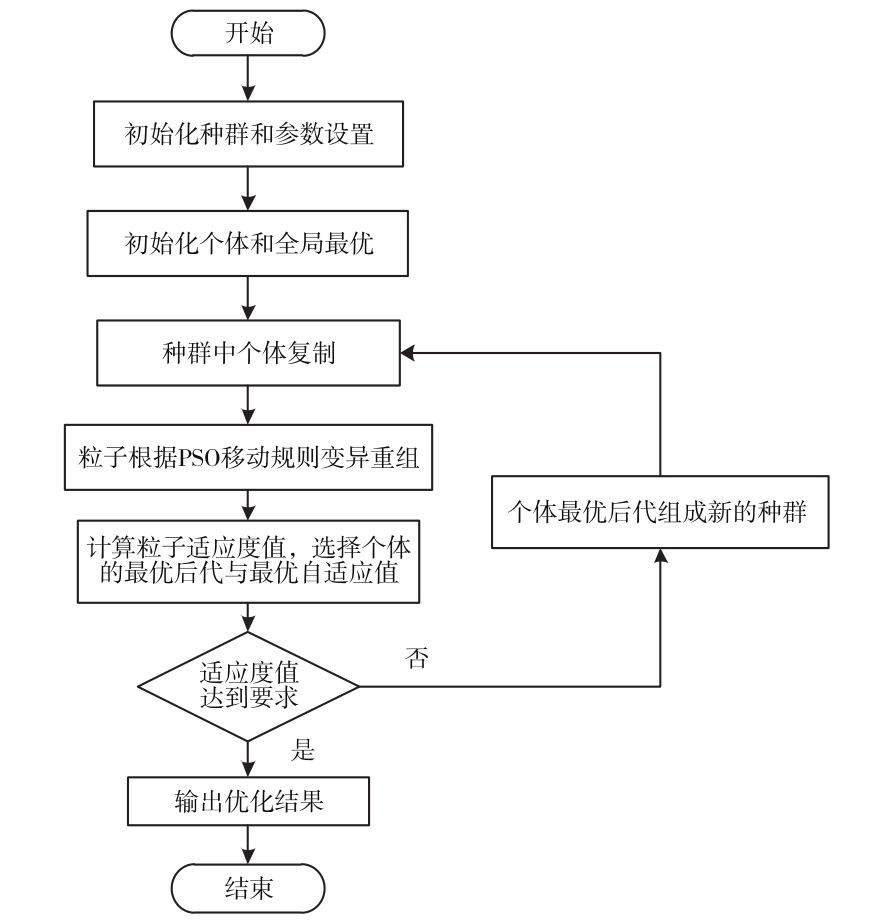
图1 进化粒子群算法流程图
1.2??应用进化粒子群算法求解发动机模型
2.2 临床指标 改良组的住院时间、创口愈合时间、疼痛程度得分少于传统组,且肛门括约肌功能评分高于传统组,差异显著(P<0.05)。见表2。
全局最优解也被随机打乱:
发动机处于某一稳态工作状态时,需要同时满足流量、功率、转速平衡等包含6个非线性共同工作方程组,要获得共同工作方程,需要从进气道入口至尾喷管出口截面按气流流过的顺序进行一次完整的计算。稳态工作点求解的数学问题实质是求解独立变量为未知数的非线性隐式方程组。

参数的变异基本规则与进化算法的规则相似:
“保密!”陆叔叔笑着说,又忙起了手中的活计。制作蜡像的过程实在漫长,小达刚开始还很有兴致,但没过多久,就有些待不住了。

图2 应用进化粒子群算法求解发动机模型流程图
输入外界大气条件和初值,进行发动机各部件热力学计算,之后求解共同工作方程,计算残差,计算进化粒子群算法的适应度函数值,根据适应度值或迭代次数判断是否终止计算。如不满足终止条件,则根据进化粒子群算法产生新的一组独立变量(ZF,ZC,PCNF,PCNC,TFFLP,TFFHP),再重复进行发动机各部件计算,直到满足终止条件,输出计算结果。
2??算例与计算结果
本文选取了在某次部件法建模过程中N-R算法迭代不收敛情况的算例来验证进化粒子群算法在发动机建模中的应用效果。
两种计算方法给出相同的设计点参数和初值。表1为进化粒子群算法的参数设置。
表1 算法初始参数设置

粒子数最大迭代次数局部学习因子全局学习因子惯性权重粒子运动编码范围(百分比转速)粒子运动编码范围(涡轮换算流量)粒子运动编码范围(部件相对压比函数)300200 2.0 2.0 0.8 [70,100] [20,200] [0.1,1]
优化目标函数为:![]()
计算结果如图3所示。
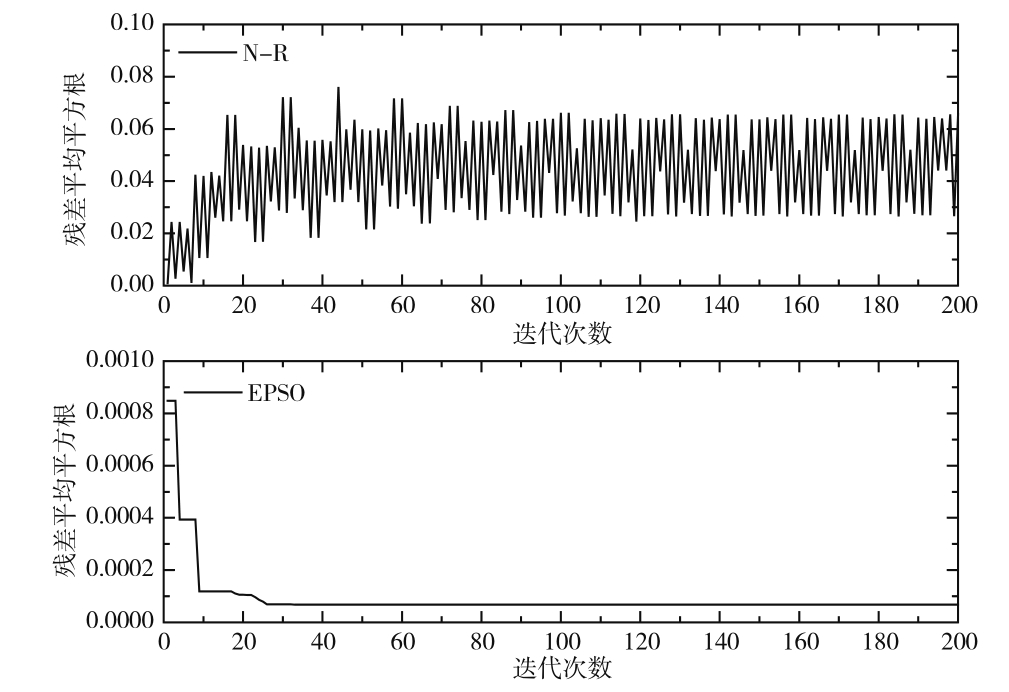
图3 残差平均平方根随迭代次数的变化
在相同初值的情况下,N-R法求解发动机模型时往往需要好的初猜想值,初猜值选取不合适经常会导致迭代过程中趋于发散,无法求解。而进化粒子群算法很快达到收敛,计算的残差平均误差平方根为6.8×10-5,达到很高的精度。
3??结论
经典算法在求解发动机模型时往往需要好的初猜想值,初猜值选取不合适经常会导致迭代计算发散。在建模过程中,调整初猜值往往没有好的办法,一般凭借经验试取,造成建模工作量大。进化粒子群算法不需要精确的初猜值,可以很快地对发动机模型求解,且有很高的精度。本文应用算例验证了基于随机搜索的现代化算法求解非线性模型具有良好的效果,具有一定的工程应用价值。
[1] 钟一文.智能优化算法及其应用研究[D].杭州:浙江大学,2005.
[2] 鲁峰,黄金泉,佘云峰,等.航空发动机状态变量模型的QPSO寻优混合求解法[J].推进技术,2011(5):25-29.
[3] 张强,李本威,马力.粒子群算法在航空发动机部件模型求解中的应用[J].系统仿真学报,2009(12):78-81.
[4] Miranda,V.,Evolutionary Algorithms with Particle Swarm Movements[C].Intelligent System Application to Power System,2005.Proceedings of the 13th International Conference on,2005,10(6):6-21.
[5] V.Miranda and N.Fonseca,Evolutionary Algorithms and Evolutionary Particle Swarm(EPSO)in modelling evolving energy retailers.[C].Proceeding of the 15th PSCC-Power System Computation Conference,Belgium,Aug 2005.
Application of Evolutionary Particle Swarm Optimization Algorithm in Aero-engine Model Solving
文章来源:《工程与试验》 网址: http://www.gcysyzz.cn/qikandaodu/2020/0512/326.html

