现在的位置:主页 > 期刊导读 >
求双跨连续梁临界载荷及固有频率的新方法
【作者】:admin【关键词】:【摘要】:连续梁在土木、机械等实际工程中得到了广泛的运用。文献[1]利用临界载荷特征方程研究了任意线弹性支承的双跨压杆稳定性,文献[2]利用梁函数及能量法求得了两等跨刚度不同连续梁
连续梁在土木、机械等实际工程中得到了广泛的运用。文献[1]利用临界载荷特征方程研究了任意线弹性支承的双跨压杆稳定性,文献[2]利用梁函数及能量法求得了两等跨刚度不同连续梁的固有频率,文献[3]采用文献[2]的计算方法求得了不等跨两跨连续弹性支座梁的固有振动频率,文献[4]采用固有频率特征方程研究了失谐连续双跨梁结构的振动特性。采用以上方法计算双跨连续梁临界载荷及固有频率的工作量都比较大,但是,采用文献[5,6]的计算方法研究双跨连续梁的弹性稳定及固有振动,可以克服文献[1-4]计算方法的不足。
1??临界载荷计算公式
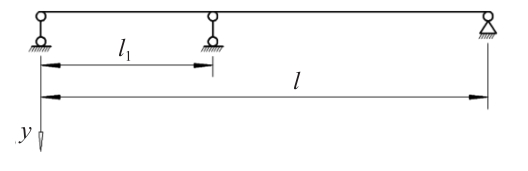
图1 双跨连续梁
对于图1所示双跨连续梁,假设其在外载荷作用下的挠度函数可用组合三角函数表示为:
式(1)中:a1,a2,a3 为待定常数。
参阅文献[7,8]可知,图1所示双跨连续梁的屈曲势能表达式为:
式(2)中:E为弹性模量;I为惯性矩;P为轴向压力。
式(3)中:
我还想设计一个手机充电口,计划在停电时给手机、平板电脑等电子产品充电,但是我掌握的知识还不够,因此没有制作。
由于中间支撑位移为:
参阅文献[7,8]可知图1所示双跨连续梁固有振动势能为:
式(4)中:η为拉格朗日系数。
把式(1)代入式(4)中可得:

2??固有频率计算公式
利用式(12)可得:
综上所述,本文结合实例分析了建筑施工项目管理过程中,安全控制的主要策略。通过安全网络体系的构件,相关安全管理制度的完善以及施工现场的安全管理执行,减少了安全事故发生的频次,确保了建筑施工项目的顺利开展。因此,相关工作人员必须重视安全管理工作,努力提高自身的安全管理意识,提高建筑工程施工阶段的安全管理水平,推动我国建筑行业的可持续发展。
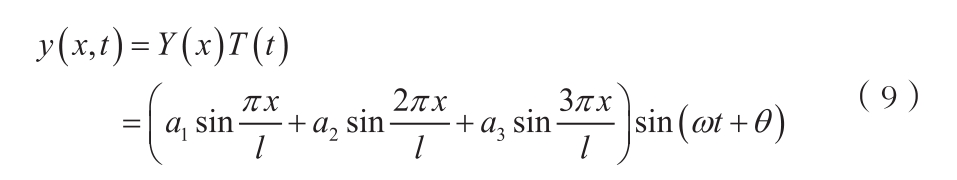
式(9)中:ω为固有频率,θ为相位,t为时间。
我一边想着、一边独自漫步在罗马街头,两边的霓虹灯总是在以出乎人意料的节奏闪烁,汽车一辆接着一辆,各种音乐的喇叭在高歌、啼叫、冷笑、哀呜。车灯闪烁而过,映得行人的脸庞阴晴不定,似滑稽剧中的角色。罗马的歌剧总是以热闹著称,每个角色都有自己的任务。街上的行人就似歌剧中的角色,匆匆赶赴自己的夜生活。罗马是一个以夜生活为目的的城市,每个人都有自己的夜生活。
利用式(2)、式(3)可构造拉格朗日函数:
式(17)中:i=1,2,…,n;n1=1,n2=1.25;N为连续梁中间支撑个数。
利用式(3)、式(10)可构造拉格朗日函数为:
把振型函数Y(x)代入式(11)中可得:
式(12)中:
图1 所示双跨连续梁固有振动时,可设其动位移为:
我期待这一天的到来,我渴望早日回报父母的养育之恩,我要让三爹和母亲看到,我今生有幸做他们的儿子,是一件多么值得骄傲的事情。
式(14)中:
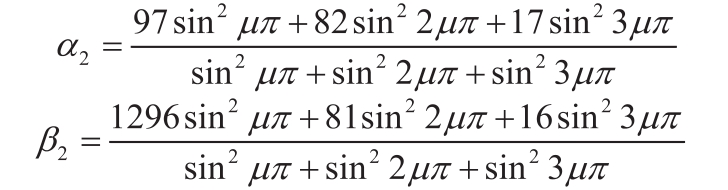
利用式(14)可得:
由式(15)可知图1所示双跨连续梁的一阶固有频率、二阶固有频率计算公式分别为:
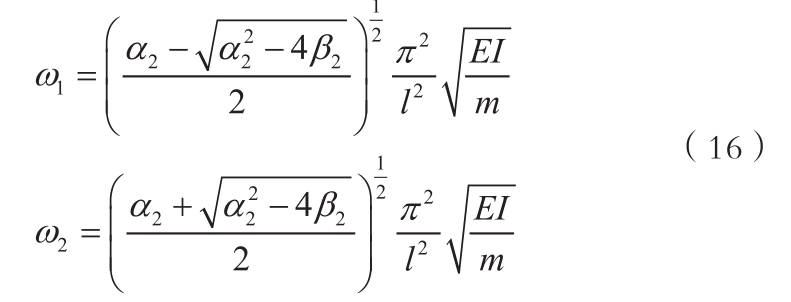
3??计算分析
为了分析本文的计算精度,把式(8)的计算结果与文献[7]的计算结果列在表1中,把式(16)的计算结果列在表2中。
利用式(3)、(13)可得:
表1 临界载荷 P

式(8) 文献[7]解 误差(%)0.5 μimages/BZ_12_533_2775_547_2796.pngimages/BZ_12_550_2782_568_2796.pngimages/BZ_12_582_2775_616_2796.pngimages/BZ_12_778_2775_793_2796.pngimages/BZ_12_795_2782_814_2797.pngimages/BZ_12_828_2775_862_2796.png0 0.4images/BZ_12_513_2870_525_2892.pngimages/BZ_12_537_2871_551_2892.pngimages/BZ_12_553_2870_567_2892.pngimages/BZ_12_569_2877_588_2892.pngimages/BZ_12_602_2871_636_2891.pngimages/BZ_12_759_2870_771_2892.pngimages/BZ_12_783_2871_796_2892.pngimages/BZ_12_799_2870_811_2892.pngimages/BZ_12_814_2877_833_2892.pngimages/BZ_12_847_2871_881_2891.png0.80 0.3images/BZ_12_513_2965_525_2987.pngimages/BZ_12_537_2965_551_2987.pngimages/BZ_12_554_2965_566_2987.pngimages/BZ_12_569_2972_588_2987.pngimages/BZ_12_602_2966_635_2987.pngimages/BZ_12_760_2965_772_2987.pngimages/BZ_12_784_2965_798_2987.pngimages/BZ_12_814_2973_832_2987.pngimages/BZ_12_846_2966_879_2987.png0.62 0.2images/BZ_12_513_3061_527_3082.pngimages/BZ_12_538_3061_551_3082.pngimages/BZ_12_554_3061_567_3082.pngimages/BZ_12_570_3068_588_3082.pngimages/BZ_12_602_3061_636_3082.pngimages/BZ_12_758_3061_772_3082.pngimages/BZ_12_783_3061_796_3082.pngimages/BZ_12_798_3061_813_3082.pngimages/BZ_12_815_3068_834_3082.pngimages/BZ_12_848_3061_882_3082.png0.36 0.1images/BZ_12_513_3156_527_3177.pngimages/BZ_12_537_3156_551_3177.pngimages/BZ_12_553_3156_568_3177.pngimages/BZ_12_570_3163_589_3177.pngimages/BZ_12_603_3156_636_3177.pngimages/BZ_12_758_3156_772_3177.pngimages/BZ_12_783_3156_795_3177.pngimages/BZ_12_800_3156_812_3177.pngimages/BZ_12_815_3163_834_3178.pngimages/BZ_12_848_3156_882_3177.png3.69
表2 固有频率

μ ω1 ω2 0.5images/BZ_12_1596_453_1611_475.pngimages/BZ_12_1613_461_1631_475.pngimages/BZ_12_1678_454_1711_475.pngimages/BZ_12_1971_453_1985_475.pngimages/BZ_12_1995_453_2009_475.pngimages/BZ_12_2011_461_2030_475.pngimages/BZ_12_2077_454_2111_475.pngimages/BZ_12_1654_444_1716_524.pngimages/BZ_12_2053_444_2116_524.png0.4images/BZ_12_1584_557_1596_579.pngimages/BZ_12_1607_557_1622_579.pngimages/BZ_12_1624_564_1643_579.pngimages/BZ_12_1690_557_1724_579.pngimages/BZ_12_1964_557_1977_579.pngimages/BZ_12_1988_557_2001_579.pngimages/BZ_12_2004_557_2016_579.pngimages/BZ_12_2019_564_2038_579.pngimages/BZ_12_2084_557_2118_579.pngimages/BZ_12_2060_547_2122_627.png0.3images/BZ_12_1576_661_1590_682.pngimages/BZ_12_1601_661_1614_683.pngimages/BZ_12_1617_661_1630_683.pngimages/BZ_12_1633_668_1651_683.pngimages/BZ_12_1698_661_1731_682.pngimages/BZ_12_1964_661_1976_683.pngimages/BZ_12_1987_661_2000_683.pngimages/BZ_12_2003_661_2017_683.pngimages/BZ_12_2020_668_2038_683.pngimages/BZ_12_2085_661_2118_682.pngimages/BZ_12_2061_651_2123_731.png0.2images/BZ_12_1577_764_1591_786.pngimages/BZ_12_1618_764_1630_786.pngimages/BZ_12_1633_772_1651_786.pngimages/BZ_12_1698_765_1731_786.pngimages/BZ_12_1964_765_1977_786.pngimages/BZ_12_1987_764_2001_786.pngimages/BZ_12_2003_764_2018_786.pngimages/BZ_12_2020_772_2038_786.pngimages/BZ_12_2085_765_2118_786.pngimages/BZ_12_2061_754_2123_834.png0.1images/BZ_12_1590_868_1604_890.pngimages/BZ_12_1607_868_1620_890.pngimages/BZ_12_1622_868_1637_889.pngimages/BZ_12_1639_875_1658_890.pngimages/BZ_12_1705_868_1738_889.pngimages/BZ_12_1964_868_1977_890.pngimages/BZ_12_1988_868_2000_890.pngimages/BZ_12_2004_868_2017_890.pngimages/BZ_12_2020_875_2038_890.pngimages/BZ_12_2085_868_2118_889.pngimages/BZ_12_2061_858_2123_938.png
由表1可知,μ=0.5时,本文式(8)的计算结果就是精确解,μ=0.4、0.3、0.2时,本文式(8)的计算结果与文献[7]的精确解误差非常小。即使μ=0.1时,本文式(8)的计算结果与文献[7]的精确解误差也仅为3.69%,没有超过实际工程所允许的误差5%。
由文献[8]可知,最左端与最右端皆为简支撑的连续梁固有振动频率公式为:
式(10)中:m为梁单位质量。
氨基酸类化合物含有氨基和羧基2种官能团,质谱条件下常产生 [M+H]+ 的准分子离子峰。查阅资料发现,大多数氨基酸(除精氨酸外)在正离子模式下会失去NH3、COOH或OH等基团,从而形成特征离子峰[10]。本品中共鉴定出7种氨基酸类化合物,分别为亮氨酸、精氨酸、丙氨酸、苏氨酸、酪氨酸、苯丙氨酸、色氨酸。
由式(17)可知图1所示双跨连续梁的一阶固有频率、二阶固有频率分别为:
秀容母亲说:“乔瞧咋咋呼呼,没半点规矩,这样的儿媳妇,我不要!她学什么不好,偏要跟父亲学医,她又不想当接生婆。我听人说过,有一回抬来一个病人,她说,我爹不在家,我来治吧,三两下就把那人衣服撕了……我知道,她是想救人,那人胸口被蛇咬了,得赶紧把毒血挤出来,但她一个姑娘家,怎能把陌生男人的衣服撕开来?”看着儿子焦急的面孔,秀容母亲放缓了语气:“其实,西大街另有一位好姑娘,你若娶了她,娘倒是很满意。”
由表2可知,![]() 时,本文方法计算的图1所示双跨连续梁一阶固有频率就是精确解,本文方法计算的二阶固有频率与式(18)的误差仅为2.34%。
时,本文方法计算的图1所示双跨连续梁一阶固有频率就是精确解,本文方法计算的二阶固有频率与式(18)的误差仅为2.34%。
从以上分析可知,本文方法研究图1所示双跨连续梁临界载荷及固有频率,不但计算精度高且计算简便,更易于工程设计人员实际工程中掌握应用。
4??结束语
为了研究图1所示双跨连续梁临界载荷及固有频率,引入拉格朗日系数构造拉格朗日函数,把拉格朗日函数对挠度函数中待定系数求极值,即可求得双跨连续梁的临界载荷及固有频率。此方法不但计算精度高且计算简便,更易于工程设计人员实际工程中掌握应用。
1)施肥比例失调。根据实地调查看,偏施氮肥、磷肥,轻施钾肥和中、微量元素肥的情况比较普遍,造成果园土壤养分失调,不利于产量和质量的提高。
构建以湟中县西堡镇为中心范围的21370hm2城市生态绿芯建设,打造成为一处自然生态净化功能大、推动城市转型升级带动力强的城市生态森林公园。筑牢以西宁南北山为生态屏障的城市生态屏障。加快湟水河、北川河、南川河三河六岸绿化,建设城市生态景观廊道。
[1] 黄开志,陈小亮.任意线弹性支承的双跨压杆稳定性计算[J].武汉工程大学学报,2014,36(9):7-11.
[2] 田敏.两等跨刚度不同钢连续梁的振动简便计算方法[J].工业建筑,2017,47(S1):257-261.
[3] 侯义娜,张荣山.不等跨两跨连续弹性支座梁的振动简便计算方法[J].工业建筑,2012,42(S1):196-202,169.
[4] 周盛林,李凤明.失谐连续双跨梁结构振动特性的理论和实验研究[J].振动工程学报,2017,30(1):149-154.
[5] 吴晓.拉格朗日函数法在静不定结构内力计算中的应用[J].空间结构,2016,22(1):25-30.
[6] 谭邹卿,杨云澜,田玉祥,等.广义变分原理在求解杆系装配应力中的应用[J].力学与实践,2017,39(2):202-205.
[7] R.C.皮萨连科,A.H.亚科符列夫,B.B.马特维也夫.材料力学手册[M].范钦珊,朱祖成,译.北京:中国建筑工业出版社,1988.
[8] 振动计算与隔振设计组.振动计算与隔振设计——工厂设计中的防振问题[M].北京:中国建筑出版社,1976.
New Method for Calculating the Critical Load and Natural Frequency of Two-span Continuous Beam
文章来源:《工程与试验》 网址: http://www.gcysyzz.cn/qikandaodu/2020/0512/333.html

