现在的位置:主页 > 期刊导读 >
利用剪应力公式研究楔形截面梁的弯曲正应力
【作者】:admin【关键词】:【摘要】:楔形截面梁在空间结构中应用比较广泛。文献[1]讨论了两端固支楔形变截面梁的热弯曲,文献[2]采用求积元法分析了楔形变截面钢-混凝土组合梁弯曲和自由振动,文献[3]研究了剪力对楔
楔形截面梁在空间结构中应用比较广泛。文献[1]讨论了两端固支楔形变截面梁的热弯曲,文献[2]采用求积元法分析了楔形变截面钢-混凝土组合梁弯曲和自由振动,文献[3]研究了剪力对楔形变截面双模量梁弯曲应力的影响,文献[4]研究了考虑剪切效应的旋转FGM从楔形梁刚柔耦合动力学建模与仿真,文献[5]研究了用楔形体解答求解矩形变截面梁及其适用范围,文献[6]研究了楔形梁腹板在弯、剪及局压联合作用下的弹性屈曲,文献[7]研究了交叉梁系结构中变截面杆件的计算问题。由以上文献可知,楔形梁是实际工程中较常见的承载构件。弹性理论采用半逆解法研究楔形梁的弯曲应力是采用多项式进行求解的,存在一题一方法一解的不足,且不能求解复杂外载荷作用下楔形梁的弯曲应力。本文利用剪应力公式研究了楔形梁弯曲正应力的求解,得到了复杂外载荷作用下楔形梁的弯曲正应力公式,弥补了弹性理论的不足。
1??楔形梁弯曲正应力
对于图1所示复杂载荷作用下的楔形梁,可用奇异函数把外载荷表示为如下载荷集度形式:
把式(1)对x积一次分可得梁截面剪力:

图1 复杂载荷作用下楔形梁
把式(2)对x积一次分可得梁截面弯矩:
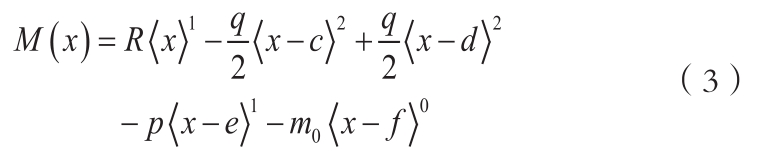
对于图1所示楔形梁,可把其截面高度表示为:
(2)优化地方环境执法监测机构。我国县级市在环境执法监测工作方面出现多部门监管现象,不仅浪费了大量行政资源,而且容易导致职能冲突,出现各种不良现象。因而,县级政府需要成立专门的环境执法监测机构,将其上司机关设为地方政府环境保护部门,实现垂直监管。在2016年9月22日,国务院发布了《关于省以下环保机构监测监察执法垂直管理制度改革试点工作的指导意见》,这也就更加需要地方政府予以部署。
利用式(4)可知楔形梁截面惯性矩及静矩分别为:
实验结果的检测方法有多种,当教材中的检测方法不能达到预期效果时,可以引导学生思考在其他实验中有没有出现过类似的问题,有没有方法可以借用。例如,在“果汁中的果胶和果胶酶”实验中,实验结果需要观察果汁的澄清度。平时的实验中,学生一般用肉眼观察,各个试管中的果汁澄清度差异很不明显。这时,教师可以启发学生联想到:在“亚硝酸盐的测定”实验中曾经使用过分光光度计来测量吸光度从而推测亚硝酸盐的含量,若在本实验中也使用分光光度计来定量检测,将定性试验改为定量试验,就可以明确地比较出不同实验组中的果汁澄清度差异。
式(4)中:

式(5)中:![]() ,b为梁宽度。
,b为梁宽度。
由材料力学可知,图1所示楔形梁截面剪应力近似公式为:
利用式(4)~式(7)可得:
为了检验式(13)的计算精度,下面以图2所示集中载荷作用下悬臂楔形梁为例,进行计算。
由文献[9]可知有下式成立:
式(7)中:G为剪切弹性模量;u为轴向位移;u(0)为中性层轴向位移;w为楔形梁弯曲挠度。
由文献[8]可知,采用式(6)计算楔形梁截面剪应力已不适用,但是可利用式(6)求得计算复杂外载荷作用下楔形梁截面通用弯曲正应力修正公式。

由文献[8]、文献[9]可知,h1=0时,图2所示悬臂楔形梁在集中载荷作用下截面最大正应力为:
2??算例分析
近年来,由于人们生育时间的推迟以及辅助生殖技术的发展,辅助生殖成为受孕困难患者的首要选择,而促排卵药物的使用导致越来越多的双胎妊娠甚至是多胎妊娠发生[1-4]。与单胎妊娠相比,双胎妊娠的染色体非整倍体发生率更高且筛查工作更为复杂,集中在双胎的合子性质对筛查的影响以及双胎更容易发生有创产前诊断的并发症等方面[1, 3, 4]。因此,急需一项创伤性小且准确有效的筛查手段解决双胎妊娠的产前筛查需求。
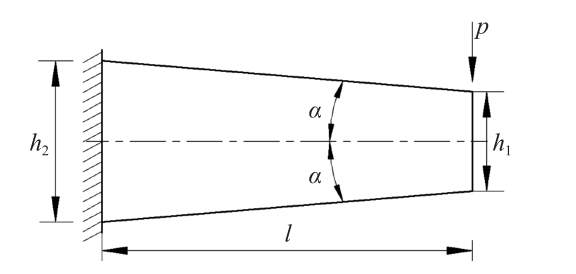
图2 集中载荷作用下楔形梁
把式(1)~式(3)代入式(13)中即为图1所示复杂载荷作用下,楔形梁弯曲正应力修正公式,此弯曲正应力修正公式是通用公式。而弹性理论仅能对单一载荷给出一题一解,存在一定的局限性。
⑤旋转复位法:患者端坐于方凳上,两腿分开,以棘突右侧偏歪为例,医者查清偏歪处后,嘱患者双手抱头,身体放松,医者右手自患者右腋下伸向前,掌部压于颈后,嘱患者坐定。助手面对患者,双腿夹住患者左腿,双手固定髋部,医者用左拇指扣住偏向右侧的棘突,用右手拉动前屈60~70度,然后向右侧弯大于45度,在最大侧旁位,医者用右手加力使患者躯干向后旋转,同时左手拇指向左上推动棘突,若手法成功,可感觉到拇指按压下的椎体轻微错动,当听到“咯嗒”响声时,复位即告成功,嘱患者卧硬板床6~8小时,每周两次。

下面把β、β’ 随半楔角α变化的数值列在表1中,以便讨论分析。
利用重复控制跟踪的统一潮流控制器抑制系统强迫振荡方法//蒋平,陈琼,吴熙,蔡晖,祁万春,谢珍建//(18):64
表1 β、β’的数值(μ=0.25)

注:表1中误差=![]()
β′ 误差(%)0° 1 1 0 10° 0.984 0.970 1.44 15° 0.964 0.947 1.79 20° 0.934 0.906 3.09 25° 0.891 0.859 3.73 30° 0.833 0.799 4.26 35° 0.755 0.733 3.00 40° 0.648 0.660 -1.84 45° 0.5 0.585 -14.53 α β
由表1可知,本文方法式(16)的计算结果与弹性理论式(17)的计算结果在半楔角α ≤ 40°即楔形角度不超过80°范围内吻合得比较好,式(16)与弹性理论式(17)计算误差均没有超过实际工程所允许的误差5%。在工程实际中,半楔角α=40°的楔形梁已经是很少见的了。
化学学习的主阵地是课堂,但是由于化学学科的应用性与社会性,教师可以进行教学的场所就不仅仅局限于课堂,生活中、社会上,到处都有可供教师使用的教学素材.教师可以组织学生进行调查研究,给定学生一个主题,让学生以小组为单位围绕给定的主题展开调查与研究.在实践主题的设计过程中,教师要根据学生的实际情况以及当地的条件,评估可行性与安全性,保证实践活动能顺利、有效地开展下去.
弹性理论式(17)仅是图2所示悬臂楔形梁当h1=0时的解析解,而本文给出的式(13)、式(15)则是图1所示在复杂载荷作用下楔形梁的弯曲正应力公式,所以说本文给出的楔形梁弯曲正应力修正公式是通式,本文方法弥补了弹性理论存在一题一方法一解的不足。
3??结论
(1)本文方法给出的楔形梁弯曲正应力修正公式的计算结果与弹性理论方法的计算结果,在半楔角α≤40°即楔形角度不超过80°范围内吻合得比较好,计算误差均没有超过实际工程所允许的误差5%。这说明本文方法给出的楔形梁弯曲正应力修正公式计算精度较高。
(2)本文给出的楔形梁弯曲正应力修正公式是通式,对任意载荷作用下楔形梁的弯曲应力计算都适用,而弹性理论的半逆解法仅适用楔形梁在单一载荷作用下的弯曲应力计算,本文方法克服了弹性理论一题一方法一解的局限性。
[1] 吴晓,刘奇元.两端固支楔形变截面梁的热弯曲讨论[J].空间结构,2018,24(1):87-90.
[2] 申志强,夏军,吴克刚,等.楔形变截面钢-混凝土组合梁弯曲和自由振动的求积元分析[J].国防科技大学学报,2018,40(1):42-48.
[3] 吴晓,罗佑新.剪力对楔形变截面双模量梁弯曲应力的影响[J].力学季刊,2017,38(4):791-800.
[4] 高晨彤,黎亮,章定国,等.考虑剪切效应的旋转FGM楔形梁刚柔耦合动力学建模与仿真[J].力学学报,2018,50(3):654-666.
[5] 刘章军,叶永,周宜红,等.用楔形体解答求解矩形变截面梁及其适用范围[J].力学与实践,2012,34(2):71-74.
[6] 李进.楔形梁腹板在弯、剪及局压联合作用下的弹性屈曲分析[D].南充:西南石油大学,2017.
[7] 黄志刚.交叉梁系结构中变截面杆件(矩形截面抛物线楔形梁)的计算问题[J].空间结构,2008(1):50-57.
[8] S.铁摩辛柯,J.盖尔.材料力学[M].北京:科学出版社,1990.
[9] 徐芝纶.弹性力学简明教程(第二版)[M].北京:高等教育出版社,1997.
Research on Bending Normal Stress of Wedge Beam by Using Shear Stress Formula
文章来源:《工程与试验》 网址: http://www.gcysyzz.cn/qikandaodu/2020/0512/334.html
上一篇:求双跨连续梁临界载荷及固有频率的新方法
下一篇:全机疲劳试验异常数据判断方法研究

